Floating-Point Numbers Demystified

Nothing brings fear to my heart more than a floating point number.

— Gerald Jay Sussman
MIT Professor

In this post, I tried to debunk common myths about floating-point numbers by explaining their subtleties, introducing each of them by showing the problem they are solving. This is a long blog post. To write it, I read several dozen articles on the subject, often shorter, but none answered all my questions. I hope it will answer yours.

Floating-Point Numbers

Let’s get started by running a few instructions using the Python interpreter:

$ python
>>> 0.1+0.2
0.30000000000000004
>>> 1.2-1.0
0.19999999999999996
>>> 0.1 + 0.1 + 0.1 - 0.3 # 0?
5.55111512313e-17

Hmm, that’s weird. A bug in Python? No. You get the same result in almost all languages, since most of them follow the same specification (a little bit about that later).

Let’s try the same test in JavaScript, directly from your browser, by simply entering javascript:alert(0.1+0.2) in the address bar. A popup appears and displays 0.30000000000000004. Too bad. The same result, which will make the hair of any math teacher stand on end. (Indeed, I’m writing this article following a discussion with a math professor that is teaching Python to his students.)

The base

First, computers are electronic devices, full of components, in particular transistors. The basic operation of a transistor is switching (on and off). In other words, it is 0 or 1. So, computers work with what is called Binary Number System in mathematics, instead of the Decimal Number System we use everyday (1 is represented as 1 in binary, 2 as 10, 3 as 11, 4 as 100, and so on).

Depending on the base (e.g., 10 or 2), there exist numbers that cannot be represented. For example, 1/3 cannot be represented as a decimal number as there is an infinite number of digits after the floating point (0.33333…). In binary system, 0.1 cannot be represented for the same reason, in the same way that 0.2 cannot neither. Why? Mathematics to our rescue.

Take the prime factors of the base (i.e., the prime numbers that can be multiplied to give the base number). For the decimal base, the prime factors are 2 and 5, since 10 = 2 * 5. When you divide a number by a prime different from one of these prime factors like 3, problems are lurking. (30/3 is OK but 10/3, 1/3, 7/3 are all failing examples that cannot be represented with the decimal system).

The larger the base, the more there are prime factors and the more there are numbers that can be represented in this base (base 30 = 2 * 3 * 5, base 10 = 2 * 5, base 2 = euh… just 2). In short, there is no worse base than binary system to represent numbers but when hardware is around, it often has the last word.

To illustrate the problem with a concrete example, consider 0.2 in base 2.

First, how do we build numbers in the decimal system? By composition. Look at this example:

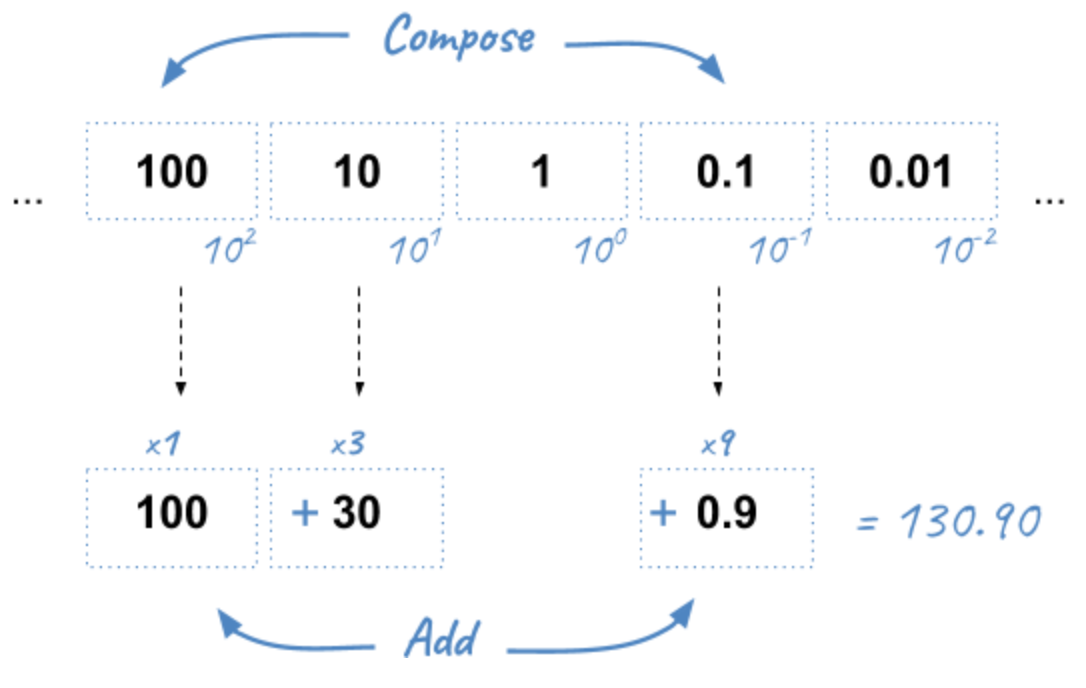
Here are the equivalent numbers on which to compose in base 2:

Let’s try to represent 25 in binary using the above table. 25 = 16 + 8 + 1 in decimal, so 10000 + 1000 + 1 = 11001 in binary. Easy.

What about 1/5? Not so easy… There is no 1/5 in the table, and there are no values we can add to get this result. Therefore, we have to approximate and use the available representable numbers. The (partial) solution is 1/8 + 1/16 + 1/128 + 1/256 + 1/2048 + 1/4096 = 0.001100110011 in binary, and 0.19995117187 in decimal. Pretty close, but not exact. These approximations will result in more rounding errors when we are going to talk about floating arithmetic in the second part of this article.

Key Takeaways

We’ve learned than, regardless the number system, there are numbers we cannot represent exactly without having to use fractions. Nobody will be surprised that 0.333333333333 is not an exact value for ⅓, but we sometimes forget computers are working with 0’s and 1’s, and when we are entering 0.1, the programming language uses the inexact binary representation instead.

Is that the only problem with floating-point numbers? Of course, not!

To finite and beyond

Computers are physical devices, with hardware limitations. Our disk and memory are limited, and thus, even the biggest machine will never be able to store the largest number (integer or floating-point number).

Moreover, the processor acts as the computer brain. It supports a specific list of instructions (e.g., ADD, DIVIDE, LOAD), which operates on fixed length operands (e.g., 32 bits, 64 bits). What this means is you can ask your processor to add two numbers as long as these numbers does not exceed a predefined size limit. If you want to add larger numbers, you have to use software code, but this considerably slows down the process. So, in practice, programming languages often add abstractions for large numbers, but for performance and implementation concerns, the basic types follows these underlying restrictions imposed by the computer hardware.

What it means for floating-point numbers to be limited in size?

In short, a maximum size limits the numbers that we may fit inside. To measure the impact of this limit, we will use decimals in the following examples because we are used to, but remember what we have just seen in the previous section, computers work with binary numbers.

Let’s try to put the number π into a fixed floating-point number:

+-------------+ size limit
| 3.141592653 | 5897932384626433832795028841971...
+-------------+

Problem. Without surprise, not all digits can be fit into the space. It’s like when you take the subway in rush hours, you may be surprised by how many people can tightly fit into it, there will always be people staying on the platform. On this example, the stored number will be rounded as the next digit is 5. Size limit is synonym with rounding errors too.

The number π is a fascinating number but there are many other floating-point numbers you may want to represent. An astronomer may want to measure the distance between planets, whereas a chemist will work with infinitesimal numbers such as the mass of an neutron. And you want to make everyone happy!

Here is the approximate distance to Mars in millimeters:

+-------------+ size limit
| 54624378953 | 679.68543445...
+-------------+

Problem. The floating point is not even included, so the number is meaningless.

Here is the approximate mass of a neutron in grams (1.675 * 10^-24 g):

+-------------+ size limit
| 0.000000000 | 000000000000001675
+-------------+

Problem. No significant digits are included… Completely useless too.

Clearly, we need a better solution to satisfy both the astronomer and the chemist, to store large and small floating-point numbers using as few digits as allowed by the machine. The solution is called Decimal floating point where a number is represented by a fixed number of significant digits (the significand) and scaled using an exponent in some fixed base. An example:

Let’s try the previous examples again using this technique.

The number π (314159 * 10^-5):

  Sign.  | exp.
+----------------+ size limit
| 314159 |    -5 |
+----------------+

Distance to Mars (546244 * 10⁸):

  Sign.  | exp.
+----------------+ size limit
| 546244 |     8 |
+----------------+

Mass of a neutron (1675 * 10^-27):

  Sign.  | exp.
+----------------+ size limit
|   1675 |   -27 |
+----------------+

That’s a lot better. We preserve the most meaningful digits. We still have the rounding problem. But numbers have meaning and are now usable. Not being able to put all your stuffs inside a box does not mean the box is useless!

There is, however, a new question to answer. If we have, for example, 32 bits to store a floating number, how many bits should be used for the significand, and how many bits should be used for the exponent. (For the base, if we always use the same base, there is no need to store it).

There isn’t a clear answer. If we allocate more bits for the significand, we get increased precision. If we allocate more bits for the exponent, we may store larger and smaller number. There is, however, a commonly accepted solution, known as the IEEE Standard 754.

Why a standard?

We need to turn the clock back to understand the motivations. Floating-point binary numbers were beginning to be used in the mid 50s. At that time, each manufacturer was deciding the number of bits and the format used by the floating-point unit (FPU), the piece of hardware responsible for making operations on floating-point numbers very fast. It was working, except if you decide to move your program to another machine, hence with a different way of representing floating numbers. The results were different (different rounding, different precision errors).

By mid 1980s, a committee was formed to standardize everything around floating-point numbers: How are they stored? How to manage exceptions such as division by 0? etc. This standard was adopted in 1985 by all computer manufacturers so that programs were portable among computers, since every floating-point arithmetic unit was implementing the standard. This explains why we were able to reproduce our initial example using different programming languages. The standard brings portability, reproducibility, and predictability.

The IEEE 754 standard provides not just one format, but different formats, such as single precision, double precision, double extended, each differing in their size (the number of bits), and thus, the total count of numbers that can be represented (without approximation). We commonly find these types in popular programming languages, like in Java, where we have the choice between float vs double (single vs double precision).

Table 1. IEEE Standard 754 Types
Type	Sign	Exponent	Significand/Mantissa	Total bits
Single	1	8	23	32
Double	1	11	52	64
Extended precision	1	15	64	80

Significand or Mantissa?

In American English, the usage of the term mantissa remains common in computing and among computer scientists. However, the term significand is encouraged by the IEEE floating-point standard and by some professionals such as Donald Knuth to avoid confusion with the pre-existing use of mantissa for the fractional part of a logarithm. We will use the term significand in this article.

Let’s try to represent π using the single precision type (32 bits in base 2).

We will see that the situation is a little more complex compared to our previous attempt. To help us, we can get the answer using the Golang method math.Float32bits like this:

package main

import (
    "fmt"
    "math"
)

func main() {
    var number float32
    number = 3.141592653589793238462
    bits := math.Float32bits(number)
    fmt.Printf("%.32b", bits)
    // 01000000010010010000111111011011
}

(Try it by yourself)

So, 01000000010010010000111111011011 is the final answer. Great, welcome to the binary system again!

Using the previous IEEE 754 table, we can decompose the answer:

 sign  exponent   significand
 +---+----------+-------------------------+
 | 0 | 10000000 | 10010010000111111011011 |
 +---+----------+-------------------------+

Where:

The sign 0 means the number is positive.
The exponent is 10000000 (2⁸) (128 in decimal).
The significand is 10010010000111111011011 (4788187 in decimal).

If we apply the formula (±) significand * 2^exponent, we get:

$ python
>>> + 4788187 * 2**128
1629335605620067578555305271434895937106870272L

Even if we don’t know the number π by heart, it’s definitely wrong. To explain this result, we need to introduce details of the standard.

The Exponent Bias

First, the standard defines an exponent bias (127 for single precision) that is added to the real exponent value. That means we need to subtract this value (128 - 127 = 1 on the previous example) to get the real exponent value.

The exponent bias is just an optimization when comparing exponents in hardware. To understand the motivations, the exponent can be positive or negative to represent both tiny and huge values, but the usual representation for signed values in computers is to add a leading bit for the sign (0 and 1 for positive and negative values). This leading bit would make the comparison harder. So, by shifting the value by 127, all values become positive (0 now means -127, 1 means -126, … 128 means 1, 255 means 128). You may safely forget the details, but remember to subtract the bias!

Let’s try to revise our previous calculation:

$ python
>>> +1 * 2**(128 - 127) * 4788187
9576374

Still wrong…

Normalized Numbers

Second, the significand is not a simple binary number, where the rightmost bit is 2⁰, then 2¹, 2², … until 2²³. The significand represents a sum of fractions where the leftmost bit is 2^-1 (1/2), then 2^-2 (1/4), 2^-3 (1/8), … until 2^-24. Basically, the floating-point is not on the right, but on the left:

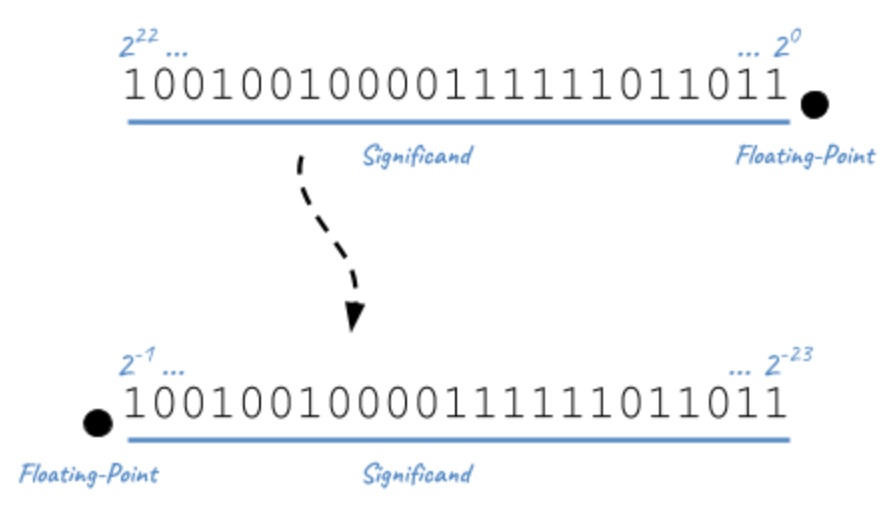
The result is a number always between 0 and 1, far different from our previous calculation.

Using our example, the significand represents:

10010010000111111011011
= 2^-1 + 2^-4 + 2^-7 + ...
= 1/2 + 1/16 + 1/128 + ...
= 0.5707963705062866

The complete calculation using Python:

$ python
>>> significand = 2**-1 + 2**-4 + 2**-7 + 2**-12 + 2**-13 + \
               2**-14 + 2**-15 + 2**-16 + 2**-17 + 2**-19 + \
               2**-20 + 2**-22 + 2**-23
>>> exponent = 128-127 # subtract the exponent bias
>>> +1 * 2**exponent * significand
1.1415927410125732

Still wrong, but closer! There is one last detail to discuss, the hidden bit.

In practice, any binary floating-point numbers can be represented as 1.ffffff x 2^exponent by adjusting the exponent. This representation is called the normalized representation, and you probably have used this technique in school with the decimal system. We learned that 0.050 × 10³ is equivalent to 0.5000 × 10², 5.000 × 10¹, and so on. When applying the same technique to binary numbers, the first bits is always 1 (except for edge cases like 0 or Infinity, more about that later in this article). With the IEEE standard 754, we must omit the initial 1 when storing the significand. This optimization gets us better precision (e.g., the saved bit is reused to represent 2^-23 in single precision).

Finally, to fix our calculation, we just need to add 1 to the significand we evaluated previously (thus, the significant is now always between 1 and 2, except for some edge cases):

$ python
# Before: +1 * 2**1 * significand
# Now:
>>> +1 * 2**1 * (1 + significand)
>>> +1 * 2**1 * (1 + 0.5707963705062866)
3.1415927410125732

That’s much better!

Key Takeaways

We’ve learned that floating-point numbers are not stored verbatim. The sign, significand and exponent are used to represent tiny and large numbers with just as few as 32 bits in single precision. The IEEE standard 754 ensures the portability between computers and programming languages by defining the number of bits for each element. We have also seen that the standard includes some optimizations important to know to correctly interpret the binary representation like the hidden bit and the exponent bias.

Are we done with floating-point numbers imprecision? I’m afraid not. We should now inspect one of the most common sources of confusion (and a major source of imprecision).

Mind the Gap

Here is a small Go program to illustrate what we are going to talk:

package main

import (
        "fmt"
)

func main() {
        var f float32
        f = 16777216.0
        if f == f+1 {
                fmt.Println("Are you serious?")
        }
}

When running this program (Try it by yourself):

Are you serious?

It’s not a bug. The good news is we have already seen everything we need to know in the previous section to be able to explain this behavior.

Why such gaps?

To illustrate the problem, we will use a dummy 4-bit floating-point type (2-bit exponent, 2-bit significand). We omit the sign bit for simplicity, but we will use the same optimizations as described by the IEEE standard 754: a hidden 1-bit and the offset bias exponent (only -1 to subtract in this case). The following list presents all the representable numbers and their decimal representations.

exponent significand binary        decimal

      00 00          1.0  * 2^-1     0.5
      00 01          1.25 * 2^-1     0.625
      00 10          1.5  * 2^-1     0.75
      00 11          1.75 * 2^-1     0.875
      01 00          1.0  * 2⁰      1.0
      01 01          1.25 * 2⁰      1.25
      01 10          1.5  * 2⁰      1.5
      01 11          1.75 * 2⁰      1.75
      10 00          1.0  * 2¹      2.0
      10 01          1.25 * 2¹      2.5
      10 10          1.5  * 2¹      3.0
      10 11          1.75 * 2¹      3.5
      11 00          1.0  * 2²      4.0
      11 01          1.25 * 2²      5.0
      11 10          1.5  * 2²      6.0
      11 11          1.75 * 2²      7.0

Our dummy 4-bit type can only represent the numbers present on this list. Any other number should be rounded to the closest number present on this list. Consequently, it’s really easy to get the kind of weird behavior highlighted previously. For example, 4.0 - 4.2 == 0 will print True because the closest number for 4.2 is 4.

Here is a diagram to visualize the gaps between these numbers:

For standard types such as single or double precision, the pattern is very similar, except there are a lot more numbers. If we add the bit sign, we just need to reflect the diagram to get something like this:

Gaps are larger and larger when numbers are getting smaller or bigger.

Let’s try to understand the logic behind these gaps.

Predict the gaps

In our Go example, 16777217.0 was not selected randomly. It’s the first integer than cannot be represented accurately. There is no magic. Let’s go deeper and understand how we could have found it ourselves.

A n-bits number can represent 2ⁿ different values. For example, with 2 bits, you can represent 2² values: 00, 01, 10, and 11. The significand contains 23 bits (+1 hidden bit), and thus, can represent 2²⁴ different numbers:

0000 0000 0000 0000 0000 0000 = 0
0000 0000 0000 0000 0000 0001 = 1
0000 0000 0000 0000 0000 0010 = 2
0000 0000 0000 0000 0000 0011 = 3
...
0000 0000 0000 0000 0010 1010 = 42
...
1111 1111 1111 1111 1111 1110 = 16777214
1111 1111 1111 1111 1111 1111 = 16777215

With the IEEE 754 format, we have seen that the significand should be normalized, so that the first bit is 1 in order to save a bit. So, in reality, we have:

42 = 0000 0000 0000 0000 0010 1010 x 2⁰
   = 0000 0000 0000 0000 0101 0100 x 2^-1
   = 0000 0000 0000 0000 1010 1000 x 2^-2
   = 0000 0000 0000 0001 0101 0000 x 2^-3
   = 1010 1000 0000 0000 0000 0000 x 2^-24
      ----------------------------
           23-bits significand

It’s exactly what we learned in school about decimals. Move the comma to the left and increase the exponent by 1, move the comma to the right and decrease the exponent by 1. Moving the comma does not change the result. It just change the representation.

The same logic is applied here with binaries. The following figure shows why integers can be safely represented using the normalized representation, using the 4-bit dummy type as the example:

Normalized or not, we can represent the same numbers when using the same number of bits.

If we apply this same logic for the single precision format (32 bits), we would find that all integers ranging from −2²⁴ to +2²⁴ may be safely represented in IEEE 754 (24 bits for the significand). Note that this is only true for integers, not decimals, because if you remember the beginning of this article, 0.1 cannot be represented.

Here are the previous examples normalized:

               23-bits significand
             -----------------------
1        = 1|00000000000000000000000 with exponent = 0
2        = 1|00000000000000000000000 with exponent = 1
3        = 1|10000000000000000000000 with exponent = 1
...
42       = 1|01010000000000000000000 with exponent = 5
...
16777214 = 1|11111111111111111111110 with exponent = 23
16777215 = 1|11111111111111111111111 with exponent = 23

So, until 16777215, everything is correct.

What about 16777216 and 16777217?

If we look more closely, their binary representation consist of 25 bits:

1000000000000000000000000
1000000000000000000000001

25 bits for 24 bits available… We have a problem. But why 16777216 is correctly represented and 16777217 is not?

Let’s begin with 16777216:

  1000000000000000000000000
= 1000000000000000000000000. x 2⁰
= 100000000000000000000000.0 x 2¹
= 10000000000000000000000.00 x 2²
...
= 1.000000000000000000000000 x 2²⁴
    -----------------------
      23-bits significand

This gives us:

0 10010111 00000000000000000000000

Where:

sign: 0 because the number is positive
exponent: 10010111 corresponding to 24 + 127 in binary
significand: 00000000000000000000000 as the first bit is hidden

No meaningless digits was lost, so 16777216 is accurately represented.

Let’s try the same operation with 16777217:

  1000000000000000000000001
= 1000000000000000000000001. x 2⁰
= 100000000000000000000000.1 x 2¹
= 10000000000000000000000.01 x 2²
...
= 1.000000000000000000000001 x 2²⁴
    -----------------------X
      23-bits significand

In IEEE 754 format:

0 10010111 00000000000000000000000

The same representation as 16777216… There is no way to fit a 25-bits number in a 24-bits space if the 25th bit is important.

What is the gap?

The smallest difference between two numbers is obtained by switching the last bit (2^-23) in the significand like this:

0 10010111 00000000000000000000000
0 10010111 00000000000000000000001

Which increment represents this change?

  2^-23 (the last bit) * 2²⁴ (the exponent)
= 2^-23+24
= 2¹
= 2

Of course! This increment explains why starting from 16777216, not all integer can be safely represented. Indeed, the next integer is 16777218, then 16777220, 16777222, and so on.

In fact, the gaps are easily predictable and depend only on the exponent value. On the previous example, the gap between two successive numbers will always be 2 as long as the exponent is 24 (or 151 with the exponent bias). When the exponent is increased to 25 (or 152 with the exponent bias), the gap becomes 2^-23 * 2²⁵ = 2² = 4. The representable numbers are 33554432, 33554436, 33554440, and so on until 67108856, 67108860.

We observe that the gap increases by the next multiple of 2 each time the exponent is incremented. To better visualise the gap, let’s try a bigger exponent to measure how large the gap becomes as numbers are getting bigger. For example, let’s try the exponent 120 (or 247 with the exponent bias):

0 11110111 00000000000000000000001

Gap = 2^-23 * 2¹²⁰
    = 2^-23+120
    = 2⁹⁷
    = 1.5845632502852868e+29
    = 158456325028528680000000000000

In practice, this means that any number between two representable numbers will be rounded to the "closest" value. For example, 1329228005784916000000000000000000000 will get rounded to 1329227995784916000000000000000000000 (that’s a huge rounding!).

We can reproduce the initial example of this section using larger numbers:

package main

import (
        "fmt"
)

func main() {
        var f float32
        f = 1.329227995784916e+36
        if f + 10000000000000000000000000000 == f {
                fmt.Printf("Equals")
        }
}

The program prints Equals (Try it by yourself).

Bonus

Before closing this section, we can apply what we learned with single precision and try to predict the first unrepresentable number in double precision. (Hint: the significand uses 52 bits over the 64 bits available for double precision instead of the 23 bits in single precision.)

Answer: If 2²⁴ + 1 is the first integer unrepresentable in single precision, 2⁵³ + 1 should be the first integer not representable in double precision:

2⁵³ + 1 = 9,007,199,254,740,993

The proof in code, using Python, where floating numbers only use the double precision format:

$ python
>>> 9007199254740993.0
9007199254740992

Bingo!

Key Takeaways

We’ve learned that floating-point types don’t just define a range of representable numbers. There exists gaps inside this interval where numbers cannot be represented, resulting in rounding. This is due to the format significand-exponent. We cannot store large and tiny numbers and be able to store everything between these extremes in a restricted number of bits. No magic.

Zero

Before moving on arithmetic, there is still a question we didn’t address. We say there is always a hidden bit whose value is 1 in the significand, or say differently, that we should add 1 to the significand (since 1 x 2⁰ = 1 x 1 = 1). But how do we represent 0?

The trick used by IEEE 754 standard is to define 0 like this:

0 for the exponent
0 for the significand
And 0 or 1 for the bit sign (positive zero vs negative zero)

So, when we have these numbers in single precision:

0 00000000 00000000000000000000000
1 00000000 00000000000000000000000

We know they should be interpresent as zero and we have to ignore the hidden bit. Easy? That’s not the end of the story.

Subnormal numbers

Let’s try to find the smallest normalized number in single precision. We know that exponent can’t be only 0 because it’s reserved for zero, so, we have:

0 00000001 00000000000000000000000

This number corresponds to:

1 x 2^(1-127) = 2^-126 = 1.1754944e-38

The next representable number is:

0 00000001 00000000000000000000001

The gap of between these two numbers is equivalent to 2^-23 * 2^-126 = 2^-149 = 1.4012985e-45.

Here are the first normal numbers (normalized numbers are also called normal numbers):

  1.175494350822286e-38
+ 1.4012985e-45 (gap)
= 1.175494490952134e-38
+ 1.4012985e-45 (gap)
= 1.175494631081980e-38
+ 1.4012985e-45 (gap)
= 1.175494771211827e-38
+ 1.4012985e-45 (gap)
= 1.175494911341673e-38
+ 1.4012985e-45 (gap)
= 1.175495051471520e-38
...

It’s not obvious but there is a huge chasm between zero and these first normal numbers. It’s not really easy to visualise it because we are talking about really small numbers, but if the distance between zero and the first normal number represents the distance Paris-New York, the distance between each successive normal number is only two feet. To fill this gap, IEEE 754 was revised to include subnormal (or denormal) numbers. The principle is simple, if the exponent is 0, the hidden bit is 0. For example:

0 00000000 00000000000000000000001
= (0 + 2^-23) x 2^-126
= 2^-23 x 2^-126
= 2¹⁴⁹
= 1.401298464324817e-45
# This is the same gap as normal numbers with the same exponent

Or,

0 00000000 11111111111111111111111
= (2^-1 + 2^-2 + ... + 2^-23) x 2^-126
= 1.1754942106924411e-38

These two numbers represent respectively the smallest and largest subnormals numbers. We observe that the gap between two subnormal numbers is identical to the gap of the first normal numbers. That’s a good news. With subnormals, we can now move from Paris to New York by increment of two feet instead of taking a plane.

Indeed, subnormal numbers solve the gap we had on the diagram when we tried to visualize representable numbers:

It is important to realise that subnormal numbers are represented with less precision than normal numbers. This is due to the presence of the leading 0, and thus leading zero bits in the significand no longer function as significant bits of precision. Consequently, the precision is less than that of normalized floating-point numbers.

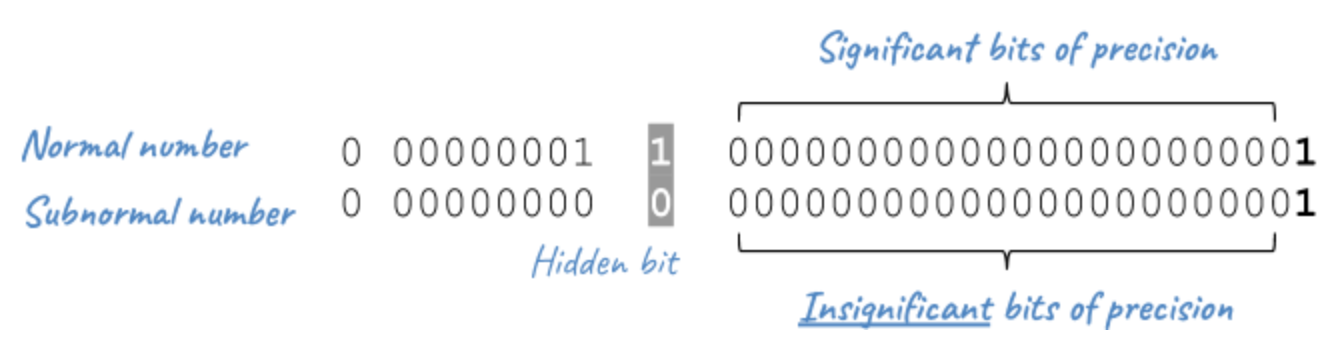
Key Takeaways

We’ve learned that subnormal numbers were introduced to fill the gap between 0 and the first normal number, and allow to represent very small positive and negative floating-point numbers.

That’s all concerning floating-point numbers. We come a long way since our initial example but there is still more to discover about the subject. Take a pause, a big breath, and let’s move on!

Floating-Point Arithmetic

Until now, we’ve only talk about floating-point numbers. We didn’t even try to add two numbers. In this part, we will face new problems when we are doing so, and will see how the IEEE standard 754 solves them.

Addition

We will reuse the first example of this article:

$ python
>>> 0.1+0.2
0.30000000000000004

These numbers are represented like this in IEEE 754:

0.1 = 0 01111011 10011001100110011001101
0.2 = 0 01111100 10011001100110011001101

Floating-point addition (or subtraction) is analogous to addition (or subtraction) using scientific notation. For example, to add 3.3 x 10⁰ to 9.985 x 10²:

Shift the decimal point of the smaller number to the left until the exponents are equal (2.5 x 10⁰ becomes 0.025 x 10²).
Add the numbers using integer addition (0.033 + 9.985 = 10.018 x 10²).
Normalize the result (1.0018 x 10³).

Let’s try the same logic on the binary numbers:

0.1 = 0 01111011 (1) 10011001100110011001101 (exp -4)
0.2 = 0 01111100 (1) 10011001100110011001101 (exp -3)

The smaller exponent is incremented and the significand is shifted right until the exponents are equal:

                                            X lost
0.1 = 0 01111100 (0) 110011001100110011001101 (exp -3) >>> shift
0.2 = 0 01111100 (1) 10011001100110011001101  (exp -3)

The significands are added using integer addition:

0.1 = 0 01111100 (0) 11001100110011001100110 (exp -3)
0.2 = 0 01111100 (1) 10011001100110011001101 (exp -3)
                ----------------------------
              = (10) 01100110011001100110011

The result is not normalized. The sum overflows the position of the hidden bit. We need to shift one bit to the right the significand and to increment the exponent in consequence:
```
0 01111100 (10) 01100110011001100110011  (exp -3)
=>
0 01111101 (1)  001100110011001100110011 (exp -2) >>> shift
                                       X lost
```

This example demonstrates we can lose precision during the operation (one bit was lost when we aligned the exponent of 0.1 and one bit was lost when we normalized the final result). Floating-point arithmetic is subject to rounding errors too. Here is the result in decimal:

$ python
(1 + 2**-3 + 2**-4 + 2**-7 + 2**-8 + 2**-11 + 2**-12 + \
     2**-15 + 2**-16 + 2**-19 + 2**-20 + 2**-23) * 2**-2
>>> 0.29999998211860657

The result differs slightly from what Python printed if we execute 0.1 + 0.2 (the result is 0.30000000000000004). There are two reasons to explain this difference. First, IEEE 754 defines rounding modes instead of just truncating the numbers like we did. The actual significand is 00110011001100110011010, and the actual value is 0.30000001192092896. Second, Python don’t use single precision but only double precision. This doesn’t solve the problem. We still have the same rounding errors but with greater precision (see below).

Rounding modes

Rounding is unavoidable when squeezing an infinite number of numbers into a finite number of bits. If a number cannot be represented, we have to use one of the representable number as a replacement. We have also seen that arithmetic operations introduce additional rounding errors too. When adding two numbers, the correct answer may be somewhere between two representable numbers. The IEEE standard 754 guarantees the same behaviour, independently of the hardware or the software, and thus, defines precisely the rounding rules.

In fact, there are several rounding modes defined by the standard: round toward positive rounds to the closest superior value, round toward negative rounds to the closest inferior value, round toward zero rounds to the closest value towards 0, and the default round to nearest (renamed round ties to even in the last standard version).

We will not go deeper on the subject. Just remember that rounding errors are unavoidable, but they are portable.

Arithmetic precision

Consider the addition of the following two numbers:

0 01111111 (1) 00000000000000000000001 = 2^-23 * 2⁰  = 2^-23
0 10011000 (1) 00000000000000000000001 = 2^-23 * 2²⁵ = 2²

The first step requires the smaller exponent to be incremented and the significand shifted right until the exponents match. This means:

0 01111111 (1) 00000000000000000000001|
0 10000000 (0) 10000000000000000000000|1
0 10000001 (0) 01000000000000000000000|01
0 10000010 (0) 00100000000000000000000|001
...
0 10011000 (0) 00000000000000000000000|100000000000000000000001
               ----------------------- XXXXXXXXXXXXXXXXXXXXXXXX
                 23 bits significand

The significand of the first number becomes zero. Therefore, the result of the addition will be equals to the second number. This example demonstrates a truncation error. If we have 24 bits for the significand in single precision (including the hidden bit), and we need to shift by more than 24 bits to align the exponent, we will inevitably lost all meaningful bits. The size of the significand determines the arithmetic precision.

In practice, 24 bits allow to represent decimal numbers until approximately 7 digits (ex: 5555555 is represented as the 23-bits representation 10101001100010101100011 in binary). This explains why we often say that the precision of single precision floating-point arithmetic is approximately 7 decimal digits. In comparison, the precision of double precision floating-point arithmetic, which uses 53 bits for the significand, is approximately 15 decimal digits (e.g., compare 0.30000001192092896 with 0.30000000000000004 in the previous section)

Overflow/Underflow

Any positive number added to the largest representable floating-point number results in overflow. Any negative number subtracted to the smallest representable floating-point number results in underflow.

Let’s see what happen precisely.

The largest single precision number is obtained by using the largest exponent and significand values:

0 11111110 11111111111111111111111
= 1.11111111111111111111111 x 2¹²⁷
= 3.4028234663852886e+38

Note: The exponent 11111111 is reserved for NaN and Inf values and cannot be used.

We will use Golang for illustration purpose, as it supports single precision floating-numbers. Here is a small program adding a small value to this large number:

package main

import (
        "fmt"
        "math"
)

func main() {
        var f1, f2 float32
        f1 = 3.4028234663852886e+38
        f2 = f1 + 1
        fmt.Printf("%.32b\n", math.Float32bits(f1)) // 01111111011111111111111111111111
        fmt.Printf("%.32b\n", math.Float32bits(f2)) // 01111111011111111111111111111111
}

The addition did nothing. It’s an example of overflow.

Infinity

Now, let’s try to add a larger number instead:

package main

import (
        "fmt"
        "math"
)

func main() {
        var f1, f2 float32
        f1 = 3.4028234663852886e+38
        f2 = f1 + float32(math.Pow(2, 103)) // 2^103
        fmt.Printf("%.32b\n", math.Float32bits(f1)) // 01111111011111111111111111111111
        fmt.Printf("%.32b\n", math.Float32bits(f2)) // 01111111100000000000000000000000
}

Unlike the previous example, we notice a difference in the result. Why? Because there was a change in magnitude. On the first example about overflow, we added a small number that doesn’t change the exponent. The result is rounded to the largest representable number, thus the value didn’t change. On this second example, we add a number that would change the exponent. By adding the product of the smallest significand (2^-24) with the current exponent (2¹²⁷), the exponent has to change, but it can’t, it’s already set to the maximum value. Rounding to the largest value is not as pertinent in this case, so a special value is returned instead, the positive infinity.

IEEE 754 standard defines positive and negative infinity using the following representations:

sign = 0 for positive infinity, 1 for negative infinity.
exponent = all 1 bits.
significand = all 0 bits.

+Inf 01111111100000000000000000000000
-Inf 11111111100000000000000000000000

This is exactly the result we got in our last example when running the Go program. We may use another example to illustrate the negative infinity:

package main

import (
        "fmt"
        "math"
)

func main() {
        var f, r float32
        f = -1
        r = f/0
        fmt.Printf("%f\n", r)
        fmt.Printf("%.32b\n", math.Float32bits(r))
}

The program prints what is defined by the standard:

-Inf
11111111100000000000000000000000

NaN

Some operations on floating-point numbers are invalid, such as taking the square root of a negative number. The act of reaching an invalid result is represented by a special code called a NaN, for "Not a Number".

Let’s try to replace the numerator by 0 in the previous example:

package main

import (
        "fmt"
        "math"
)

func main() {
        var f, r float32
        f = 0
        r = f/0
        fmt.Printf("%f\n", r)
        fmt.Printf("%.32b\n", math.Float32bits(r))
}

The result has changed to return NaN instead:

NaN
11111111110000000000000000000000

Why this special value? Without NaN, the program would have to abort completely to report the error. In practice, however, it sometimes makes sense for a computation to continue despite encountering such a scenario, so NaN let the programmer decides if the program should go on. (For example, Go has a method math.IsNaN() to check the value.)

All NaNs in IEEE 754 have this format:

sign = either 0 or 1.
exponent = all 1 bits.
significand = anything except all 0 bits (since all 0 bits represents infinity).

So, all of the following representations are valid NaN examples:

0 11111111 00000000000000000000001
1 11111111 00000000000000000000001
1 11111111 10000000000000000000000
0 11111111 11111111111111111111111

In fact, there are a lot a possible representations for NaNs: 2^23-1 for single precision (23 bits for the significand) if we omit the bit sign. That’s a lot of valid combinaisons!

The IEEE standard interprets differently these two representations:

1 11111111 00000000000000000000001
1 11111111 10000000000000000000000

If the first bit of the trailing significand is 0, we have a quiet NaN (qNaN). If it is 1, we have a signaling NaN (sNaN). Signaling means an exception should be raised, whereas quiet means NaN should be propagated through every arithmetic operation without signaling an exception (it is always possible to raise an exception at the end of the calculation if we want, as the NaN information is preserved). Semantically, qNaN's denote indeterminate operations, while sNaN's denote invalid operations. When programming in most of the languages, you are only using qNaN and have to test the value with an utility method like the math.IsNaN in Go.

Why so many representations for NaNs?

The quiet/signaling distinction imposes only two representations (1 11111111 00000000000000000000001 and 1 11111111 10000000000000000000000 are sufficient). The standard doesn’t explicit what can be done with all of these additional representations. These remaining bits are called the payload and can be use to provide context about the origin of the error. But this isn’t the only known use.

A known technique, called NaN-boxing, is implemented by some interpreters like JavaScriptCore, to pack other types such as pointers (48-bits) or integers (32-bit) inside the space left by NaNs in double precisions (where the significand represents 52 bits). As a variable can be of any type, the interpreter uses only double precision floating-points to store everything. If it’s a floating-point, it uses the usual IEEE 754 representation. If it’s another type, it uses the available 51-bits for 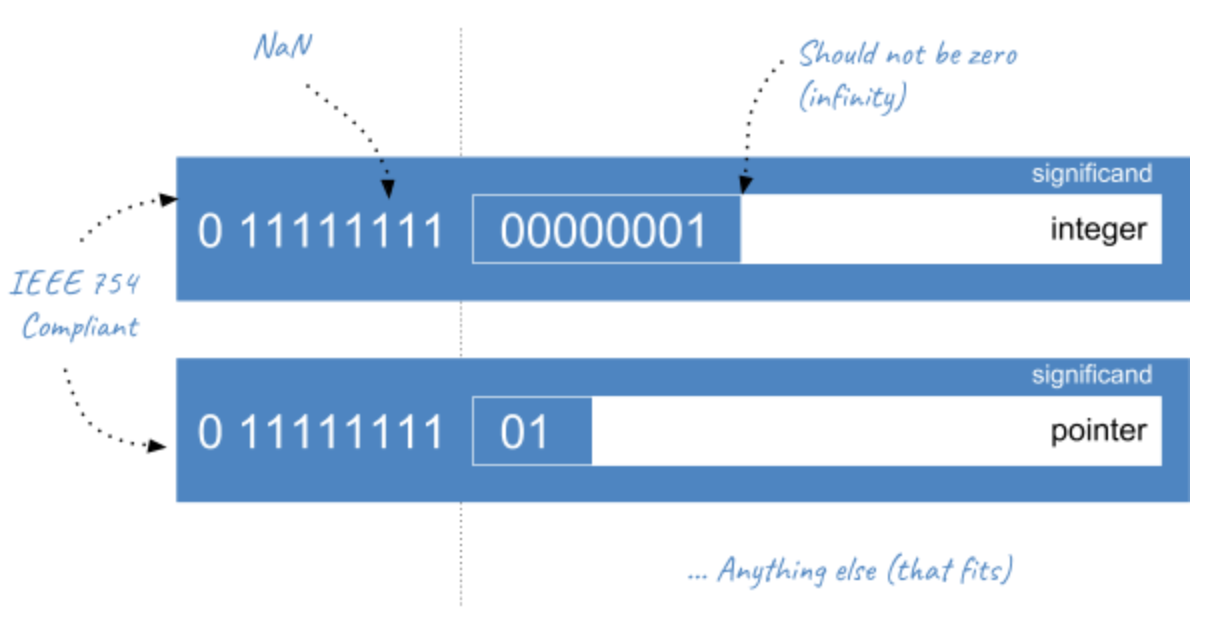NaNs to store any value (a pointer address, an integer, etc). If you want to know more about this hack, you can start looking at this great article.

Figure 1. NaN-Boxing

Key Takeaways

We’ve learned that the IEEE Standard 754 defines special formats to represent Zero, Infinity, and NaN. When you see all 0-bits or all 1-bits in the exponent, you know there is something special about that number.

We have also learned that floating-point arithmetic may result in exceptions: invalid operations like the square root of a negative number return NaN, a division by zero returns ±Infinity, an addition/subtraction/multiplication may result in overflow/underflow when the exponent would be smaller or larger than the allowed value, and we should not forget that rounding is omnipresent.

When I started writing this article, I was not prepared to go so far on the subject. We covered a large scope of the standard. If you decide to pore over it, you will see we have introduced almost every detail. We didn’t talk about the hardware implementation, or how software uses the processor instructions, but they are very low-level details, and they aren’t part of the standard anyway. I think we should stop here, and digest everything we have learned. If you want to know more about the subject, you may try this detailled article, or why not read a full book on the subject!

Conclusion

The IEEE committee succeeded in defining a standard followed by every manufacturer that make floating-point numbers predictable when porting a program between different computers, or even when copying a code snippet between programming languages. But IEEE 754 does not hide the complexity of working with floating-point numbers. Joel Spolsky, co-founder of Stack Overflow, said in 2002: "All non-trivial abstractions, to some degree, are leaky." Floating-point numbers are the perfect example of a leaky abstraction. They act as a black box most of the time, but you occasionally have to open it to avoid damages.

For a lot of applications, numbers describe measurements, which are inherently inexact. Adding rounding to the equation may be acceptable, but when you are able to compute a more accurate result in your head than your computer can, floating-point numbers are clearly not an acceptable solution.

By understanding the underlying logic behind the standard, you are now better equipped to decide if floating-point numbers are usable for your use case, or if you should use language extensions offering precise arithmetic at the expense of decreased performance.

Myths vs Reality

Myth: I can use floating-point numbers to represent common numbers like amounts. Wrong. Floating-point numbers cannot represent simple numbers such as 0.1 or 0.2.
Myth: I will not have problems if I use double precision (64 bits). Wrong. Problems are identical, but less frequent. Gaps are smaller but there are rounding errors too, and numbers such as 0.1 cannot be represented with floating-point numbers, single or double precision.
Myth: Floating-point numbers approximation only affects insignificant digits after the floating-point. Wrong. Not all integers can be represented. There exists gaps, even for relatively small values like 16,777,217 when using single precision.

About the author

Julien Sobczak works as a software developer for Scaleway, a French cloud provider. He is a passionate reader who likes to see the world differently to measure the extent of his ignorance. His main areas of interest are productivity (doing less and better), human potential, and everything that contributes in being a better person (including a better dad and a better developer).

Read Full Profile